APPROXIMATION BY ANALYTICAL FUNCTIONS OF THE TEMPERATURE DEPENDENCE COPPER ATOMIC HEAT CAPACITY IN THE INTRVAL 50-1300 K
АППРОКСИМАЦИЯ АНАЛИТИЧЕСКИМИ ФУНКЦИЯМИ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ АТОМНОЙ ТЕПЛОЁМКОСТИ МЕДИ В ИНТЕРВАЛЕ 50–1300 K
JOURNAL: «SCIENTIFIC NOTES OF V.I. VERNADSKY CRIMEAN FEDERAL UNIVERSITY. Biology. Chemistry» Volume 10 (76), №3, 2024
Publication text (PDF): Download
UDK: 536.631
AUTHOR AND PUBLICATION INFORMATION
AUTHORS:
Sheikh-Zade M.-I., Fevzi Yakubov Crimean Engineering and Pedagogical University, Simferopol, Crimea, Russia Federation
TYPE:Article
DOI:https://doi.org/10.29039/2413-1725-2024-10-3-341-348
PAGES:from 341 to 348
STATUS:Published
LANGUAGE:Russian
KEYWORDS: heat capacity, temperature dependence, approximation.
ABSTRACT (ENGLISH):
Theory and experiment show that the atomic heat capacities at constant volume and constant pressure depend on temperature. In a theoretical consideration of heat capacity, it is easier to calculate , since depends only on the change in internal energy, and also depends on the work of expansion. The dependence of on temperature for bodies with an atomic lattice was theoretically considered by Debye, who obtained a formula that correctly conveys this dependence. In an experimental determination of heat capacity, it is easier to measure the values of . In this paper, the problem of approximating the temperature dependence of the copper atomic heat capacity in the temperature interval 50–1300 K by analytical functions is considered. It is shown that in the temperature interval 300–1300 K, this dependence is satisfactorily described by the linear function
,
the parameters of which are determined by the least squares method; the standard deviation was found to be equal to s = 4·10–3.
In the interval 50–300 K, the dependence of on temperature is nonlinear and the Lagrange interpolation polynomial and cubic spline S3(T) were used to describe this dependence. It is shown that when using the spline S3(T) with the confidant aк,j, given in the table
|
K |
aK,0 |
aK,1 |
aK,2 |
aK,3 |
|
0 |
5,86 |
0,234 |
0 |
–9,896·10–6 |
|
1 |
16,32 |
0,160 |
–1,484·10–3 |
5,143·10–6 |
|
2 |
22,59 |
0,017 |
5,836·10–5 |
–0,195·10–6 |
it is possible to obtain a better approximation quality than when using the Lagrange interpolation polynomial L3(T).
ВВЕДЕНИЕ
Теплоёмкость представляет собой одну из важных характеристик вещества. Чтобы можно было сравнивать разные вещества по теплоёмкости, теплоёмкость нормируют на единицу массы вещества (удельная теплоёмкость, , Дж/(K·кг)) или на один моль вещества (молярная теплоёмкость, , Дж/(K·моль)). В случае твёрдых веществ с атомной кристаллической решёткой теплоёмкость С т называют атомной теплоёмкостью. Различают атомную теплоёмкость при постоянном объёме и при постоянном давлении . При теоретическом рассмотрении теплоёмкости легче вычислить , так как определяется только изменением внутренней энергии, а зависит ещё от работы расширения. В случае экспериментального определения теплоёмкости, легче измерять значения , так как при нагревании твёрдых тел трудно сохранить постоянство объёма тела (что необходимо для измерения значений ).
Теория и эксперимент показывают, что теплоёмкость зависит от температуры. Зависимость от температуры для тел с атомной кристаллической структурой была теоретически рассмотрена П. Дебаем [1–3], который получил формулу, правильно передающую эту зависимость. Температурную зависимость экспериментально найденных величин можно описать аналитическими функциями в различных интервалах температур.
Целью данной работы является аппроксимация аналитическими функциями температурной зависимости атомной теплоёмкости меди в интервале 50–1300 K.
МАТЕРИАЛЫ И МЕТОДЫ
Для построения приближающих функций, описывающих температурную зависимость меди, необходимо иметь в распоряжении экспериментальные значения в исследуемом интервале температур. Такие данные были заимствованы из справочников [4–6]. При температурах выше 300 K зависимость от температуры имеет линейный характер. Для нахождения параметров этой линейной зависимости был применён метод наименьших квадратов, а в качестве наилучшего приближения была использована величина выборочного среднеквадратического отклонения:
,
где N – число экспериментальных точек, – ордината k-той экспериментальной точки, – значение приближающей функции для k-той экспериментальной точки.
В интервале 50–300 K зависимость от температуры имеет нелинейный характер и для аппроксимации этой зависимости были использованы интерполяционный полином Лагранжа L3(T) и интерполяционный кубический сплайн S3(T) [7–9]. Кубические сплайны получили наиболее широкое применение на практике, так как имеют на всём отрезке аппроксимации непрерывные производные до второго порядка включительно, что обеспечивает достаточную гладкость таких сплайнов для большинства практических задач. Построение интерполяционных полиномов Лагранжа и кубических сплайнов можно производить с помощью ПК с использованием соответствующих программ [10, 11].
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
На рис. 1 представлены графически в виде точек экспериментальные значения меди при различных температурах в интервале 50–1300 K.
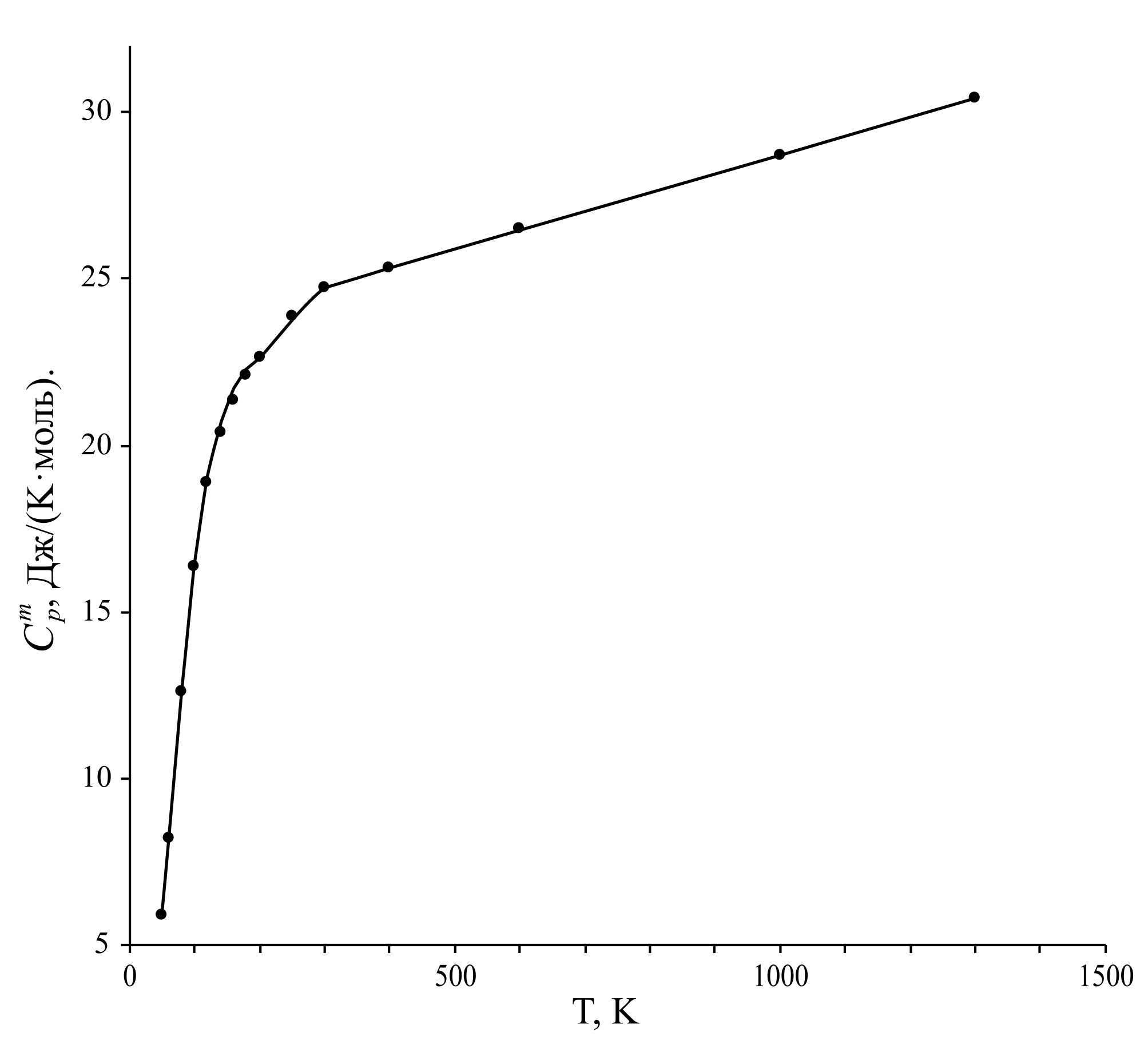
Рис. 1. Экспериментальные значения меди (точки) и их аппроксимация аналитическими функциями (сплошная линия).
Как видно из рис. 1, зависимость от температуры является сложной функцией и на практике такую зависимость при достаточно высоких температурах выражают обычно в виде различных степенных рядов [12–14]. Коэффициенты таких рядов определяются из экспериментальных данных, например, методом наименьших квадратов и помещают в справочники с указанием интервала температур, в которых соответствующий ряд даёт хорошее приближение. Чаще всего используется степенной ряд:
(1)
В [15] для меди в интервале температур 298–1356 K приведены значения коэффициентов ряда (1): a=22,64; b=6,28·10–3; c’=0. В [16] для меди в том же интервале температур приведены значения: a=22,65059; b=6,28020·10–3; c’=0. Незначительные отличия в значениях коэффициента a могут быть обусловлены, возможно, различными исходными данными для . Так как в данной работе использованы значения из [4–6], то для интервала температур 300–1300 K были определены значения коэффициентов ряда (1) методом наименьших квадратов и они оказались равными: a=22,988; b=5,679·10–3; c’=0 с значением среднеквадратического отклонения s=4·10–3. Нижняя точка (300 K) этого температурного интервала близка к стандартной температуре 298 K и к характеристической температуре Дебая для меди ΘD=313 K [15]. Как видно из рис. 1 (сплошная линия), линейная зависимость с найденными значениями коэффициентов a и b удовлетворительно передаёт зависимость меди от температуры в интервале 300–1300 K.
Из рис. 1 также видно, что ниже 300 K зависимость от температуры более сложная и ряд (1) непригоден для описания этой зависимости. Для описания такой зависимости в области температур 50–300 K можно применить классический метод решения подобной задачи – использовать интерполяционные полиномы Лагранжа [9–11]. В данной работе в качестве узлов интерполяции выбраны точки 50, 100, 200, 300 K. Поэтому в качестве приближающей функции использован кубический интерполяционный полином Лагранжа L3(T). Результат такой аппроксимации приведён в табл. 1, где в третьем столбце , а в четвёртом столбце ΔL=–.
Таблица 1
Экспериментальные и вычисленные по L3(T) и S3(T) значения теплоёмкости меди и разности Δ=–
|
T, K |
, Дж/(K·моль) |
, Дж/(K·моль) |
|||
|
выч. по L3(T) |
ΔL |
выч. по S3(T) |
ΔS |
||
|
50 |
5,86 |
5,86 |
0 |
5,86 |
0 |
|
60 |
8,16 |
8,51 |
–0,35 |
8,19 |
–0,03 |
|
80 |
12,55 |
12,94 |
–0,39 |
12,61 |
–0,06 |
|
100 |
16,32 |
16,32 |
0 |
16,32 |
0 |
|
120 |
18,83 |
18,79 |
0,04 |
18,96 |
–0,13 |
|
140 |
20,33 |
20,51 |
–0,18 |
20,66 |
–0,33 |
|
160 |
21,34 |
21,61 |
–0,27 |
21,67 |
–0,33 |
|
180 |
22,09 |
22,26 |
–0,17 |
22,23 |
–0,14 |
|
200 |
22,59 |
22,59 |
0 |
22,59 |
0 |
|
250 |
23,85 |
23,01 |
0,84 |
23,57 |
0,28 |
|
300 |
24,69 |
24,69 |
0 |
24,69 |
0 |
Из табл. 1 можно видеть, что между узлами интерполяции происходит осцилляция полинома L3(T), т.е. отклонение от экспериментальных значений в ту или иную сторону. Такая осцилляция может быть существенной при использовании полиномов Лагранжа высокой степени. Уменьшить осцилляцию можно путём уменьшения степени полинома, интерполируя только часть точек. Тогда для всего множества точек получается составная кривая, которая непрерывна на всём интервале задания точек. Такая идея реализуется также при использовании сплайнов, которые представляют собой гладкие кусочно-полиномальные функции с однородной структурой, т. е. составленные из алгебраических полиномов одной и той же степени. На практике чаще всего используют кубические сплайны. В данной работе использованы естественные кубические сплайны S3(T) [10] с узлами T0=50 K, T1=100 K, T2=200 K, T3=300 K и имеющие вид:
,
где каждый Pк(T) – многочлен третьей степени:
Pк(T) = aк,0 + aк,1·(T–Tк) + aк,2·(T–Tк)2 + aк,3·(T–Tк)3
для Tϵ[Tк, Tк+1] и к = 0,1,2.
Коэффициенты aк,j (j=0,1,2,3) находятся с использованием экспериментальных значений [10, 11]. Значения коэффициентов aк,j, найденные по методике, изложенной в [10], приведены в табл. 2.
Таблица 2
Значения коэффициентов aк,j полиномов PК(T) сплайна S3(T)
|
K |
aK,0 |
aK,1 |
aK,2 |
aK,3 |
|
0 |
5,86 |
0,234 |
0 |
–9,896·10–6 |
|
1 |
16,32 |
0,160 |
–1,484·10–3 |
5,143·10–6 |
|
2 |
22,59 |
0,017 |
5,836·10–5 |
–0,195·10–6 |
Вычисленные с использованием сплайна S3(T) значения и разности
ΔS =– представлены в табл. 1 в пятом и шестом столбцах соответственно, а в графическом виде приведены на рис. 1 в интервале температур 50–300 K (сплошная линия). Следует отметить, что в масштабе рис. 1 графическое представление результатов аппроксимации полиномом Лагранжа L3(T) невозможно отличить от графического представления результатов аппроксимации кубическим сплайном S3(T). Поэтому о качестве аппроксимации этими методами можно судить по данным табл. 1 и значений среднеквадратических отклонений s=0,319 и s=0,175 при аппроксимации полиномом L3(T) и сплайном S3(T) соответственно. Из табл. 1 и значений s можно видеть, что качество аппроксимации кубическим сплайном S3(T) лучше, чем полиномом Лагранжа L3(T).
Из полученных данных следует, что температурную зависимость меди в интервале температур 300–1300 K можно описать линейной зависимостью
,
а в интервале температур 50–300 K – интерполяционным кубическим сплайном S3(T) с коэффициентами aк,j, приведённым в табл. 2. Подобным образом можно получить аналитические выражения для описания температурной зависимости для других веществ с атомной кристаллической решёткой.
ЗАКЛЮЧЕНИЕ
Показано, что температурная зависимость меди в кристаллическом состоянии удовлетворительно описывается линейной зависимостью в интервале температур 300–1300 K, а в интервале 50-300 K более лучшее качество аппроксимации удаётся получить при использовании интерполяционного кубического сплайна S3(T), чем интерполяционного полинома Лагранжа L3(T).
- Sokolv A. A., Loskutov Yu. M., Ternov I. M. Quantum mechanics, 638 p. (Prosveshhenie, Moscow, 1965). (in Russ.).
- Zhukhoviczkij A. A., Shvarczman L. A. Physical chemistry, 520 p. (Metallurgiya, 1968). (in Russ.).
- Zhdanov G. S. Solid state physics, 502 p. (Izd-vo MSU, Moscow, 1962). (in Russ.).
- Physical quantity: handbook. Ed. Grigor’eva I.S. and Mejlikhova E. Z., 1232 p. (Energoatomizdat, Moscow, 1991). (in Russ.).
- Tables of physical quantity. Handbook. Ed. Kikoin I. K., 1006 p. (Atomizdat, Moscow, 1976). (in Russ.).
- Brief Handbook of physical and chemical quantity. Ed. Ravdel’ A. A. and Ponomaryova A. M., 232 p. (Chemistry, Leningrad, 1983). (in Russ.).
- Ahlberg J. N., Nilsson E. N., Walsh J. L. The theory of splines and their applications, 316 p. (Mir, Moscow, 1972). (in Russ.).
- Kornejchuk N. P. Splines in theory of approximation, 352 p. (Nauka, Moscow, 1984). (in Russ.).
- Zav’yalov Yu. S., Kvasov B. I., Miroshnichenko V. L. Methods of spline functions, 352 p. (Nauka, Moscow, 1980). (in Russ.).
- Mathews J. H., Fink K. D. Numerical methods. Using MathLab, 720 p. (Vil’yams, Moscow, 2001). (in Russ.).
- Lapchik M. P., Ragulina M. I., Henner E. K. Numerical methods, 384 p. (Akademiya, Moscow, 2007). (in Russ.).
- Course of physical chemistry, Vol.1. Ed. Gerasimov Ya. I. 592 p. (Chemistry, Moscow, 1979). (in Russ.).
- Bornaczkij I. I. Foundations of physical chemistry, 344 p. (Metallurgiya, Moscow, 1971). (in Russ.).
- Stromberg A. G., Semchenko D. P. Physical chemistry, 480 p. (Higher School, Moscow, 1973). (in Russ.).
- Brief Handbook of physical and chemical quantity. Ed. Mishhenko K. P. and Ravdel’ A. A., 200 p. (Chemistry, Leningrad, 1974). (in Russ.).
- Physical and chemical properties of elements. Handbook. Ed. Samsonov G. V., 808 p. (Naukova Dumka, Kiev, 1965). (in Russ.).

