COMPARATIVE ANALYSIS OF SOME FUNCTIONS USED TO APPROXIMATE THE CONTOURS OF SPECTRAL LINES
СРАВНИТЕЛЬНЫЙ АНАЛИЗ НЕКОТОРЫХ ФУНКЦИЙ, ПРИМЕНЯЕМЫХ
ДЛЯ АППРОКСИМАЦИИ КОНТУРОВ СПЕКТРАЛЬНЫХ ЛИНИЙ
JOURNAL: «SCIENTIFIC NOTES OF V.I. VERNADSKY CRIMEAN FEDERAL UNIVERSITY. Biology. Chemistry» Volume 10 (76), №2, 2024
Publication text (PDF):Download
UDK: 535.338.334
AUTHOR AND PUBLICATION INFORMATION
AUTHORS:
Sheikh-Zade M.-I. Yakubov Crimean Engineering and Pedagogical University, Simferopol, Crimea, Russia Federation
TYPE:Article
DOI:https://doi.org/10.29039/2413-1725-2024-10-2-309-315
PAGES:from 309 to 315
STATUS:Published
LANGUAGE:Russian
KEYWORDS: spectral line, contour, approximation.
ABSTRACT (ENGLISH):
Optical spectroscopy is widely used in various fields of chemistry. The main information from the spectra is obtained on the basis of data on the characteristics of spectral lines – wavelength and optical density at the maximum of the line, the shape of the contour of the spectral line. The analysis shape of the spectral line contour allows us to obtain data on interatomic interactions in radiation sources, on the mechanisms of broadening of spectral lines, remotely to determine the temperature and pressure of the gaseous medium and other information. Therefore, the study of the shape of spectral lines contours is an important task of theoretical spectroscopy.
To describe the shape of spectral lines contours, the Lorentzian function, the Gaussian function, the linear combination f(η,x) of the Lorentzian and Gaussian functions, and the Voigt function are used. In this paper, a comparative analysis quality of approximation of the long-wave branch experimental contour of the spectral line λ=3125,67Å mercury atoms by these functions, as well as an empirical function, which in normalized form shown below:
,
where x=2(λ–λ0)/δλ; λ,λ0 – the wavelength at an arbitrary point and at the maximum of contour respectively; δλ – the width of the contour at half its height; n – the parameter to be found for the contour under study. The function f(n,x) has properties: at n=2 it turns into a Lorentzian function, and at n→∞ it turns into a Gaussian function.
The least squares method was used to evaluation the quality of the approximation of the experimental contour, and the value of the sample standard approximation S was used as the criterion for the best approximation. From the analysis of the results obtained, it follows that in terms of the quality of approximation of the long-wave branch of the studied experimental contour, these functions are arranged in the following order: Voigt function, S=89·10–4; function f(n,x), S=95·10–4; function f(η,x), S=100·10–4; Lorentzian function, S=153·10–4; Gaussian function, S=613·10–4, where S is the sample standard deviation.
ВВЕДЕНИЕ
В различных областях химии широко используются физические методы исследования строения свойств атомов, молекул, строения и свойств вещества в различных агрегатных состояниях [1–3]. Весьма эффективными среди этих методов являются спектроскопические методы. Достойное место в ряду спектроскопических методов занимает оптическая спектроскопия. Основную информацию из спектров получают на основе данных о характеристиках спектральных линий, таких как: длина волны и оптическая плотность в максимуме линии, ширина линии, распределение энергии в пределах спектральной линии, которое определяет контур спектральной линии. Это относится и к характеристикам полос поглощения, когда используется абсорбционная спектроскопия. Анализ формы контура спектральных линий позволяет получить данные о межатомных взаимодействиях в источниках излучения, о механизмах уширения спектральных линий [4, 5], дистанционно определить температуру и давление газовой среды [6] и т.п. Форма контуров полос в колебательных спектрах жидкостей может быть источником информации о межмолекулярных взаимодействиях в таких средах. Из сказанного видно, что исследование формы контуров спектральных линий и полос поглощения является важной задачей теоретической спектроскопии.
Целью работы является сравнительный анализ качества аппроксимации экспериментального контура спектральной линии λ=3125,67Å атомов ртути некоторыми известными функциями, которые применяются при решении подобных задач, а также эмпирической функцией f(n,x).
МАТЕРИАЛЫ И МЕТОДЫ
В качестве контура для тестирования приближающих функций выбран экспериментальный контур линии 3125,67Å атомов ртути, соответствующий переходу между уровнями 63Р1 – 63D1 [4]. В графическом виде этот контур приведён в работе [6]. Для проведения вычислительных процедур этот контур был оцифрован. Для оценки качества аппроксимации экспериментального контура приближающей функцией был применён метод наименьших квадратов, а в качестве критерия наилучшего приближения была использована величина выборочного среднеквадратического отклонения [7]:
где N – число экспериментальных точек, yj – ордината j-той экспериментальной точки, fj(x) – значение приближающей функции для j-той экспериментальной точки. Наилучшей приближающей функцией будет функция, для которой значение S будет минимальным. Для представления контуров в графическом виде, эти контуры приводились к нормализованному виду, т.е. к центрированному и нормированному к единице по интенсивности в максимуме виду:
где x=2(λ–λ0)/δλ; λ,λ0 – длина волны в произвольной точке и в максимуме контура соответственно; δλ – ширина контура на половине её высоты;
D, D0 – оптическая плотность при λ и λ0 соответственно. Для задач, решаемых в данной работе, нет необходимости проводить аппроксимацию всего контура приближающей функцией, достаточно ограничиться одной половиной контура. Для этих целей была использована длинноволновая (ДВ) ветвь экспериментального контура.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Для аппроксимации контуров спектральных линий нередко применяют функцию Коши, которая описывает радиационное (естественное) уширение спектральных линий [4, 5]. Радиационная ширина спектральных линий равна 1,17·10–4Å и является малой величиной по сравнению с шириной спектральных линий, обусловленной другими причинами. Х. А. Лорентц показал (цитируется по [8]), что столкновения излучающих атомов с другими атомами приводит к значительно большему уширению спектральных линий. Контуры линий, уширенных по такому механизму, описываются функцией Лорентца. ДВ ветвь экспериментального контура спектральной линии λ=3125,67Å атомов ртути, построенная на основе данных работы [6], приведена в нормализованном виде на рис. 1. На рис. 1. также показан результат аппроксимации этого контура функцией Лорентца (пунктирная линия), S=153·10–4.
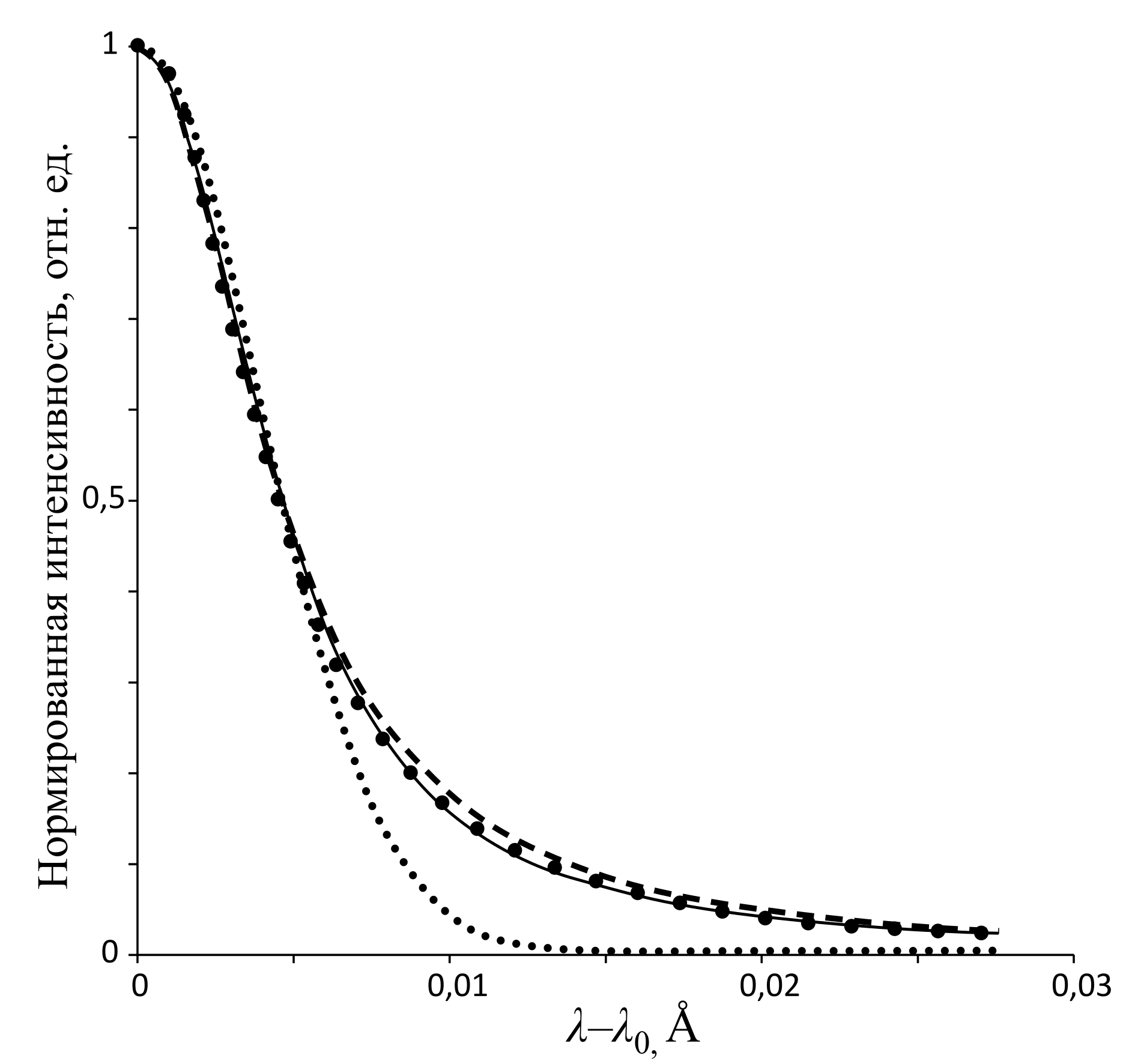
Рис. 1. ДВ ветвь экспериментального контура линии λ=3125,67Å атомов ртути (крупные точки) и его аппроксимация функциями Лорентца (пунктирная линия), Гаусса (точечная линия), функцией f(η,x) (сплошная линия).
Тепловое движение излучающих атомов является ещё одной причиной уширения спектральных линий, которое называется допплеровским уширением. Контур линий с таким механизмом уширения описывается функцией Гаусса [4, 8]. На рис. 1 показан результат аппроксимации функцией Гаусса ДВ ветви экспериментального контура (точечная линия), S=613·10–4. Как из рис.1, так и из значений S можно видеть, что качество аппроксимации ДВ ветви данного экспериментального контура функцией Гаусса ниже, чем функцией Лорентца, особенно в области крыла контура. Из рис. 1 также видно, что экспериментальный контур расположен в области между контурами Лорентца и Гаусса. Такой характер расположения экспериментального контура спектральных линий является типичным. Это наводит на мысль использовать в качестве приближающей функции линейную комбинацию функции Лорентца fЛ(x) и функции Гаусса fГ(x) [9, 10]:
(1)
Функция f(η,x) обладает предельными свойствами: при η=0 превращается в функцию Гаусса, а при η=1 превращается в функцию Лорентца. Если задачу аппроксимации экспериментального контура рассматривать как чисто математическую задачу, то η в выражении (1) можно рассматривать как подгоночный параметр, который можно найти методом наименьших квадратов. Значение η, найденное таким методом, оказалось равным: η=0,8436. Результат аппроксимации экспериментального контура функцией (1) с η=0,8436 показан на рис.1 (сплошная линия), S=100·10–4. Из рис.1 и из значений S видно, что функция (1) лучше описывает ДВ ветвь данного экспериментального контура, чем отдельно взятые функции Лорентца или Гаусса. Отметим, что функция (1) применяется и для аппроксимации контуров полос поглощения в ИК области спектра. В работе [11] показано, что контур полосы колебаний ν5 (ν=764 см–1) жидкого хлороформа удовлетворительно описывается функцией (1) с η=10/13.
Одновременное и независимое друг от друга действие двух механизмов уширения спектральных линий – лорентцевский и допплеровский, учитывает и функция Фойгта (см., например, в [4, 8]), которая может описывать контуры от гауссового при a=0 до лорентцевского контура при a→∞, где a – параметр функции Фойгта. Параметр a должен быть предварительно найден для изучаемой спектральной линии. На рис. 2 показан результат аппроксимации ДВ ветви экспериментального контура (точки) функцией Фойгта (сплошная линия), выполненный в работе [6]. Рассчитанное для этого случая значение S=89·10–4.
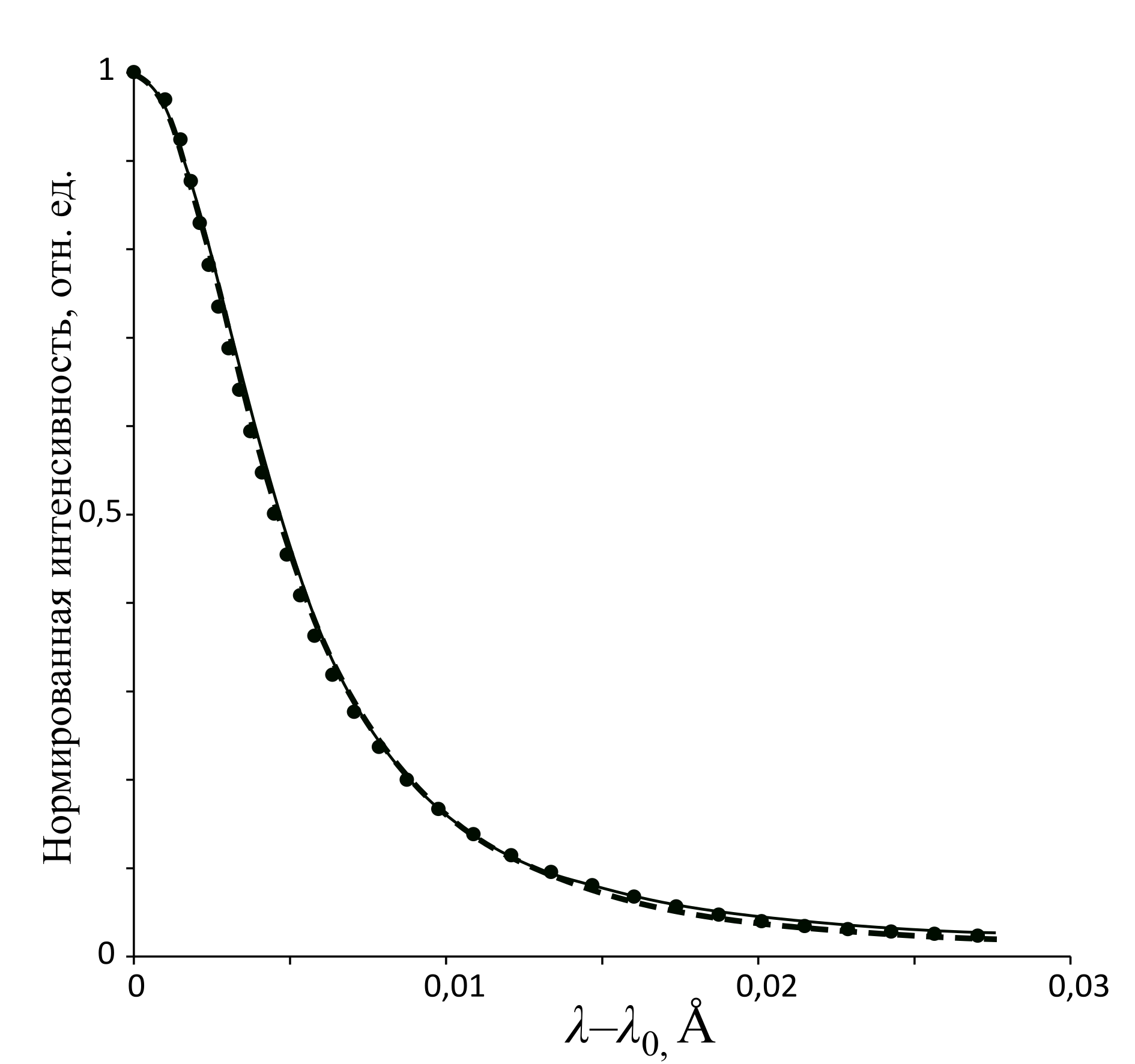
Рис. 2. ДВ ветвь экспериментального контура линии λ=3125,67Å атомов ртути (точки) и его аппроксимация функцией Фойгта (сплошная линия) и функцией f(n,x) (пунктирная линия).
Если аппроксимацию данного экспериментального контура рассматривать как чисто математическую задачу отыскания удовлетворительной приближающей функции, то можно попытаться применить для этих целей эмпирическую функцию:
,
где n – параметр, значение которого должно быть найдено для аппроксимируемого контура. Функция f(n,x) обладает предельными свойствами: при n=2 превращается в функцию Лорентца, а при n→∞ превращается в функцию Гаусса. В силу эмпирического характера функции f(n,x), вопрос о физической интерпретации этой функции здесь не рассматривается. На рис. 2 приведён результат аппроксимации ДВ ветви экспериментального контура функцией f(n,x) (пунктирная линия), которая при n=2,35 обеспечивает минимальное значение S=95·10–4. Из рис. 2 и значений S видно, что функция Фойгта наиболее удовлетворительно описывает рассматриваемый экспериментальный контур. Функция f(n,x) близка по качеству аппроксимации к функции Фойгта, хотя и несколько уступает ей.
ЗАКЛЮЧЕНИЕ
Проведён сравнительный анализ качества аппроксимации ДВ ветви экспериментального контура спектральной линии λ=3125,67Å атомов ртути пятью приближающими функциями: Лорентца, Гаусса, f(η,x), Фойгта, f(n,x). Показано, что по качеству аппроксимации эти функции располагаются в следующем порядке: функция Фойгта, f(n,x), f(η,x), функция Лорентца, функция Гаусса.
- Brand J., Eglinton G., Application of spectroscopy to organic chemistry, 279 p. (Mir, Moscow, 1967). (in Russ.).
- Atkins P. W., Physical chemistry, 584 p. (Mir, Moscow, 1980). (in Russ.).
- Smith A., Applied infrared spectroscopy, 328 p. (Mir, Moscow, 1982). (in Russ.).
- Frish S. E., Optical atom spectra, 656 p. (Lan’, Moscow, 2010). (in Russ.).
- Korolyov F. A., Theoretical optics, p. 123 (Higher school, Moscow, 1966). (in Russ.).
- Naumova N. N., Khokhlov V. N., Temperature and gas pressure determination by spectral line Voigt profiles, Opt.Zhurn., 73(8), 23(2006). (in Russ.).
- Mathews J. N., Fink K. D., Numerical methods. Using Mathlab, 720 p. (Vil’yams, Moscow, 2001). (in Russ.).
- Mitchell A., Zemansky M., Resonance radiation and exited atoms, 285 p. (ONTI, Moscow, 1937). (in Russ.).
- Whiting E. E., An empirical approximation to the Voigt profile, J. Quant.Spectrosc.Radiat.Transfer., 8, 1379(1968).
- Kielkopf J. F., New approximation to the Voigt function with applications to spectral-line profile analysis, J.Opt.Soc.Am., 63(8), 987(1973).
- Cyashhenko Yu. P., Shape of vibration absorption bands of liquid chloroform and bromoform, Opt.and Spectr., 11(2), 192(1961). (in Russ.).

